First, I'll start by saying this isn't some homework assignment, this is one of those rare, real-life problems.
I made this web page cause I'v had to explain the problem so many times.

Sorry if I use a capital L as the angle symbol...

- A robot (R) is on a field with 3 positioning beacons (A, B, and C)
- The robot knows the real-world positions (x, y) of the 3 beacons.
- The robot is able to scan around it and obtain the angles, between the 3 beacons, the scanning process also identifies the beacons (it knows which is which) It CANNOT get information on its distance from it to the beacons due to hardware limitations (via financial limitations)

The goal is to calculate the position of the robot (Rx,Ry) from the 3 angles (L ARB, L BRC, L ARC)



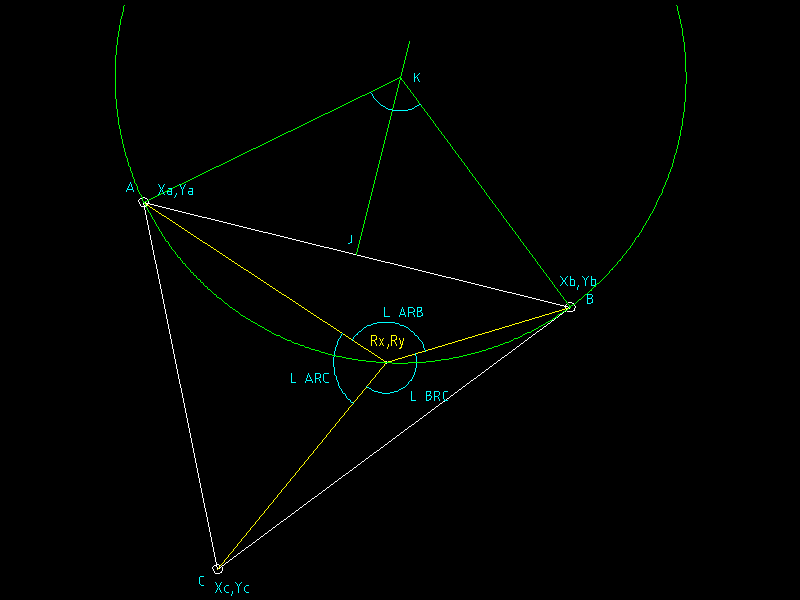
Angles that are known
L ARC
L BRC
L ARB
L ABC
L ACB
L BAC

Distances that are known
AB
BC
AC

Things that might be of help I'v worked out so far (the maybe-not-so-obvious)

>  L RCB + L RBC = L ARC + L ARB - 180
>  L RCA + L RAC = L ARB + L ARC - 180
>  L RAB + L RBA = L BRC + L ARC - 180

>  L RAB = 360 - L RCB - L ABC - L BRC - L ARB
>  L RBC = 360 - L RAC - L ACB - L ARC - L BRC
>  L ABR = 360 - L ACR - L BAC - L ARB - L ARC

An idea is to get two angles such as L RCB and L RBC, form two line equations based on their slope and the fact they pass through C and B, and calculate the intersection point.

• Credits to lhf of #math who pointed out the following:

1) - If line JK is created such that its a perpendicular bisector of line AB
2) - Then creates lines AK and BK such that L AKB = 360 - 2*(L ARB)
3) - Then draw a circle with center on intersection of JK and AK that passes through A and B
4) -> Point R will lie on that circle, if the same is done for beacons B and C, the two intersections will be the beacon in common (B) and the robots position (R)

step 2 seems kinda trickey till ya tear it apart a little more. JK bisects L AKB and JK is perpendicular to AB, so with some quite simple math, L JAK = L ARB - 90

• Credits to DWarrior of #math who took a successfull, yet round about style of the following, that lead me to the answer.

1) Sine rule: AR/sin(L ABR) = AB/sin(L ARB)
2) Sine rule: AR/sin(L ACR) = AC/sin(L ARC)
3) isolate 1 for AR:   AR = AB(sin(L ABR)/sin(L ARB)
4) isolate 2 for AR:   AR = AC(sin(L ACR)/sin(L ABC)
5) equate AR = AR:  AB(sin(L ABR)/sin(L ARB) = AC(sin(L ACR)/sin(L ABC)
6) isolate for L ABR:   sin(L ABR) = (AC/AB) * (sin(L ARB)/sin(L ARC)) * sin(L ACR)
7) pull our knowns togethor to simplify:  M = (AC/AB) * (sin(L ARB)/sin(L ARC)
     therefore: sin(L ABR) = M * sin(L ACR)
8) now, using the other 6 rules above, we can translate ABR into ACR so that everything is expressed in terms of one unknown ( L ACR ) . I'm going to drop the L symbol for this. Note that angle XYZ is same as angle ZYX

The translation loop is as follows:  ABR<->CBR<->RCB<->RCA<->CAR<->RAB<->ABR

ABR->ACR

a) given: ABR + CBR = ABC
b) re-arange: ABR = ABC - CBR
c) given: 180 - BRC = RBC + RCB
d) re-arange: RBC = 180 - BRC - RCB
e) substitute: ABR = ABC - (180 - BRC - RCB)
f) clean: ABR = ABC - 180 + BRC + RCB
g) given: RCB + ACR = BCA
h) re-arange: RCB = BCA - ACR
i) substitute: ABR = ABC - 180 + BRC + BCA - ACR

Done. ABR is expressed as ACR being the only unknown

we had:  sin(L ABR) = M * sin(L ACR)

9) re-express in terms of L ACR:  sin( L ABC - 180 + L BRC + L BCA - L ACR) = M * sin(L ACR)
10) pull knowns again to simpify: D = (L ABC - 180 + L BRC + L BCA )
      therefore:  sin( D - L ACR) = M * sin(L ACR)
11) Use rule sin(a-b) = sin(a)cos(b) - cos(a)sin(b):  sin(D)cos(L ACR)-cos(D)sin(L ACR) = M sin(L ACR)
12) seperate knowns and unknowns:
      sin(D)cos(L ACR) = M sin(L ACR)+cos(D)sin(L ACR)
      sin(D)cos(L ACR) = sin(L ACR) * (M + cos(D))

     sin(D)/(M + cos(D)) = sin(L ACR)/cos(L ACR)

13) apply sin(a)/cos(a) = tan(a): sin(D)/(m+cos(D)) = tan(L ACR)
14) arc it: ACR = atan(sin(D)/(M+cos(D)))

done! thats the trickey angle

so: 
ACR = atan(sin(D)/(M+cos(D)))
D = (L ABC - 180 + L BRC + L BCA )
M = (AC/AB) * (sin(L ARB)/sin(L ARC)

now that the anlges of the lines that intersect at the robot are known, (and points as they go through the beacons) we can solve for the position of the robot by calculting the line intersecion.

trick now is to traslate that all to math that a 16mips 8 bit machine can do in under 0.5 seconds.

 Rue